Issue #157 - Finding the Optimal Vocabulary

Vocabulary Learning via Optimal Transport for Neural Machine Translation
Introduction
Neural machine translation (NMT) models typically operate with a fixed vocabulary and address the open vocabulary problem with the help of subword segmentation algorithms (Sennrich et al., 2016; Kudo and Richardson, 2018; Provilkov et al., 2020) that allow a word to be represented as a sequence of characters, if necessary. Despite promising results, most existing subword approaches only consider frequency while the effects of vocabulary size are neglected. In today’s blog post, we will take a look at the work of Xu et al. (2021) who propose a simple and lightweight solution to generate the optimal vocabulary. One way to find the optimal vocabulary is to do full training and testing which is not very efficient and involves high computational costs. To address this problem, the authors propose a VOcabulary Learning approach via optimal Transport (VOLT) that can be used to find a well-performing vocabulary with higher BLEU and smaller size.
The Approach
Key factors of vocabulary
- Information Per Char (IPC) - Semantic meanings per char, smaller entropy value is better and helps for the model learning.
- Size - Smaller is better, fewer parameters, less rare tokens.
Between the 2 factors of vocabulary, an increase in vocabulary size leads to a decrease in cross-entropy which benefits the model learning process. On the other hand, a larger vocabulary may lead to parameter explosion and token sparsity which doesn’t help the model learning.
An alternative perspective on Vocabulary
According to the concept of Marginal Utility in economics Samuelson (1937), Marginal Utility is the amount of benefit that we can get from an increase in cost. This factor is used to balance the benefit and the cost. The authors utilize this idea by considering the factors, IPC as benefit and size as the cost, to solve the vocabulary learning problem by making use of Marginal Utility of Vocabularization(MUV) as the optimization objective.
Definition of Marginal Utility of Vocabularization (MUV)
MUV is defined as the negative derivative of entropy to vocabulary size. In order to maximize MUV, the problem reduces to finding the optimal tradeoff between the entropy and vocabulary size.
A learning-based solution to maximize MUV - VOLT
The authors define vocabulary construction as a discrete optimization problem whose target is to find the vocabulary with the highest MUV. Intuitively, this optimization problem can be solved by a series of transport processes that transports the chars into token candidates i.e start from the vocabularies with fixed sizes and search for the optimal vocabulary.
Optimal transport is about finding the best-transporting mass from the char distribution to the target token distribution with the minimum work defined by (P, D) where P is the transport matrix, and D is the distance matrix.
There are 2 steps to find the optimal vocabulary:
- Search for the optimal vocabulary with the highest entropy at each timestep t.
- Enumerating all the timesteps and selecting the vocabulary that has the maximum MUV score.
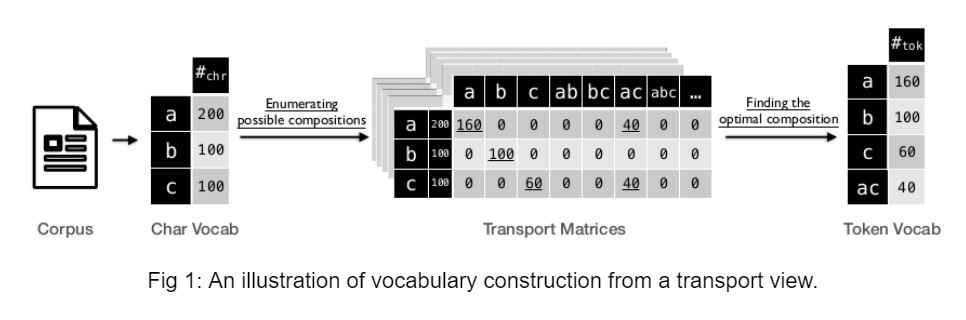
After generating the vocabulary, VOLT uses a greedy strategy to encode the texts similar to BPE. It first splits sentences into character-level tokens and then merges two consecutive tokens into one token if the merged one is already present in the vocabulary. This process is carried out until no more tokens can be merged. This way the Out-of-vocabulary tokens will be split into smaller tokens.
Datasets
To evaluate the performance of the proposed approach, the authors conduct experiments on three datasets including WMT-14 English-German translation Ott et al. (2018), TED bilingual translation and TED multilingual translation. The TED data is used from Qi et al. (2018).
Findings
- To validate the use of MUV as the vocabulary measurement, the authors carry out experiments on 45 language pairs (X-En) from TED data and calculate the spearman correlation score between MUV and BLEU scores.
- Based on the results, it can be inferred that MUI and BLEU are correlated on two-thirds of tasks. Based on the comparison between VOLT and dominantly used BPE-30K setting, VOLT achieves higher BLEU scores across the majority of the language pairs along with a significantly larger size reduction.
- Based on the comparison between VOLT and BPE-1K on an X-to-English bilingual low-resource setting, vocabularies searched by VOLT are on par with heuristically-searched vocabularies in terms of BLEU scores.
- VOLT achieves better BLEU scores than BPE-60K (most popularly used setting) across the majority of the language pairs on Multilingual MT settings.
- Based on comparisons between VOLT and BPE-Search across different vocabulary sizes, VOLT seems to be more efficient in terms of both computing power and time taken.
In summary
Xu et al. (2021) make use of the concept of Marginal Utility in economics to define an alternate perspective on vocabulary. They propose a simple and efficient vocabulary search approach - VOLT, to find the optimal vocabulary without the need for trial training. Experiments show that VOLT can effectively find a well-performing vocabulary in diverse settings.

