Issue #175 - Twenty Years of Neural Language Models and Counting

The Concept of a Language Model 

A language model (LM) represents the likelihood that a word will appear next in a text given the previous words in that text. LMs are a classic paradigm in natural language processing, tracing all the way back to when Claude Shannon described their foundation in the 1951 paper “Prediction and Entropy of Printed English”. Early approaches to LMs explicitly counted the occurrence of discrete word sequences (i.e. n-grams) in text corpora and computed probability distributions directly from the normalized counts. Current state-of-the-art LMs rely on neural network architectures, where the probability distributions are computed from continuous vectors instead of discrete counts. These architectures have become increasingly complex, but they all still perform the same function: they take a word sequence as input and output the probabilities of the next word. 

In today’s post, I’ll highlight a paper by Sun & Iyyer (2021) that reconsiders the original design of neural LMs from almost twenty years ago and examines its relevance to current state-of-the-art LMs. Before discussing this specific paper, I’ll give some general background on how neural LMs have evolved over time. 

Using Neural Networks in Language Models 

The figure below illustrates the broad scheme of an LM based on a neural network. Neural networks are represented as layers, as shown by the red and blue groups in the figure. These layers are continuous vectors that result from multiplications between weight parameters (e.g. W and U in the figure) and other layers. At the lowest layer, a neural LM encodes a sequence of discrete input words as continuous vectors, often referred to as word embeddings. Subsequent layers integrate these embeddings and further transform them into latent representations. The top layer applies a final transformation that outputs probabilities for all words that could follow in the input sequence. The LM learns this probability distribution by observing words in a corpus of training texts. During training, the weights are optimized to output probabilities that reflect the actual frequencies of the words in the corpus. 

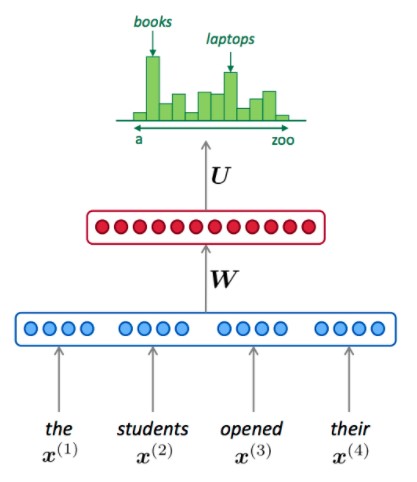Source: https://web.stanford.edu/class/cs224n/slides/cs224n-2019-lecture06-rnnlm.pdf 

In 2003, Bengio et al. presented the first practical demonstration of a neural LM. In this model, referred to here as the NPLM (neural probabilistic language model), each word in a sequence of n words was encoded as an embedding. In their experiment, the value n was set to 5. The embeddings were concatenated and transformed via a nonlinear feedforward layer. A softmax layer was then applied to yield a probability distribution predicting the subsequent (6th) word in the sequence. Computational constraints made it difficult to scale the input sequence to longer than 5 words. This was always acknowledged as a limitation, since predicting plausible words often requires knowing their context further back than the previous few words. Obviously, human utterances are conditioned on this context: in the above example, knowing that the text “The teacher asked them to read a Wikipedia article, so” precedes “the students opened their” should ideally increase the probability of “laptop” as the next word. Expanding this context became the primary challenge that motivated the development of new LM architectures. Advancements first came from Recurrent Neural Networks (Mikolov et al., 2010), and then more recently from the Transformer architecture (Vaswani et al., 2017). The key innovation of Transformers is a mechanism called self-attention, by which an embedded word can simultaneously observe all other words within the same input text, as visualized below. 

Source: https://ai.googleblog.com/2017/08/transformer-novel-neural-network.html 

In this example, when computing the probability of the word “it”, the model specifically attends to the words that most influence this probability. The word “animal” particularly increases the probability that “it” will appear in this position, so the weights associated with “animal” are activated more strongly for this prediction. Note that self-attention in LMs has a constraint not depicted in the figure: a word is only allowed to attend to previous words on its left, not future words on its right, since future words are the ones that must be predicted. Self-attention is implemented as a series of layers that comprise an encoding function alternative to that of the NPLM feedforward layers, which are not designed to facilitate this selective attention. With modern computing, self-attention is scalable to long input sequences, so word predictions can be influenced by the prior few sentences or even paragraphs. Transformer LMs obtained massive gains on the standard evaluation metric of perplexity, which scores how well an LM predicts words in new texts it has not previously seen (worse scores mean the LM is more “perplexed” by a text). This success suggested Transformer LMs could be used not just for predicting a single word in a text, but for generating an entire text from scratch. LMs were previously considered a very weak approach to text generation, but this changed when Transformer LMs like GPT-2 (Radford et al., 2019) began to perform tasks like document summarization, question answering, and story generation. 

Comparing NPLMs and Transformer LMs 

Self-attention was remarkably innovative, but other factors have contributed to the success of Transformer LMs as well. Importantly, computing frameworks have evolved since NPLMs were first introduced. LMs are now trained on much larger datasets, contain several more weights and layers, and utilize optimizations not specific to self-attention. The use of NPLMs faded simultaneously while these factors progressed. In the paper “Revisiting Simple Neural Probabilistic Language Models”, Sun & Iyyer (2021) investigated to what degree these factors affect the gap between NPLMs and Transformer LMs. More precisely, how much is self-attention itself responsible for LM performance? To investigate this, the authors examined various modifications to the NPLM and Transformer LM architectures. They used WikiText-103, a corpus of Wikipedia articles, to train the LMs and evaluate their perplexity. Note that perplexity is an inverse measure of performance, so lower scores are better. 

Improving NPLMs 

The first main finding of the paper is that the original NPLM can be significantly enhanced through features that are not specific to self-attention. The authors demonstrate this by comparing the model’s perplexity with and without these features. 

Model Size: When the NPLM is scaled from 1 layer with a total of 32M weight parameters to 16 layers with a total of 148M parameters, perplexity improves from 216 to 41.9. 

Gradient Flow Optimizations: Residual connections (He et al., 2016) allow encoded text representations to “skip” from one layer to a subsequent non-adjacent layer. This turns out to be an important optimization for the NPLM: without it, perplexity worsens from 41.9 to 660. The specific choice of optimization algorithm also makes a difference. Newer optimization methods like Adam (Kingma & Ba, 2015) enable models to learn faster than the classic Stochastic Gradient Descent (SGD) method used by the original NPLM. When SGD is used instead of Adam, perplexity worsens from 41.9 to 418.5. 

Context Length: The original NPLM was constrained to only observing five-word sequences. With hardware advancements, it is possible to include more words in the NPLM input. The result of 41.9 is achieved when the context length is 50 words. This steadily worsens as the length is reduced, all the way to 87 when the input sequence contains only 3 words. 

The authors found one additional optimization that benefited the NPLM, which was applying a 1-D convolution to the word embedding layer. This improved the perplexity from 41.9 to 31.7. By comparison, the standard Transformer LM obtained 25.0. This indicates that while the NPLM can be massively optimized beyond its original implementation, it still cannot fully replicate self-attention. 

Re-assessing Transformer LMs 

The authors then considered modifications to the standard Transformer LM. In particular, they added some constraints to self-attention to bring the model architecture closer to that of the simple NPLM. They compared the perplexity achieved by the modified architectures to that of the standard Transformer LM. 

Transformer-N: Self-attention typically consists of multiple layers, by which the model attends not just directly to the word representations, but also to subsequent encoded representations where attention has already been applied. As one modification, termed Transformer-N, the authors assessed the importance of self-attention on the initial word embeddings by instead concatenating the embeddings and applying a simple feedforward layer. Self-attention was still applied in the subsequent layers. This yielded a slightly improved perplexity, from 25.0 with the standard Transformer to 24.1 with the Transformer-N. 

Transformer-C: As discussed, the benefit of self-attention is that it can directly observe all words in an input sequence. However, it is possible that not all layers of the LM require self-attention over the entire encoded sequence. The authors examined limiting self-attention at the input embedding layer to a fixed window of words instead of the full sequence. In this modification, called Transformer-C, the lowest self-attention layer was constrained so that the representation for a given word only attended to the previous 5 words in the sequence. The results showed that this constraint slightly helped the model, again bringing the perplexity from 25.0 with the standard Transformer to 24.1 with the Transformer-C. 

Both results show that some flexibility can be afforded in the design of self-attention at the lower layers of the model. The simpler transformations performed by the NPLM at these layers yield sufficient representations for the higher-level layers. It may even be the case that these representations are advantageous relative to self-attention in capturing short-range dependencies in text. 

The Importance of Context 

LM prediction performance is highly dependent on the texts used for evaluation. This can be understood with respect to human performance on the word prediction task. For some types of text, readers may be able to predict which will occur next by just reading a few words. An example is “chocolate ice _____”, where many English speakers would say “cream” is highly likely to appear in this final position. Predictions for other texts may require a longer memory of what was previously read. An extreme example is a fiction novel where a character introduced in the first chapter doesn’t reappear until several chapters later. Human readers may be able to anticipate mentions of the character despite this contextual distance, while even state-of-the-art LMs would be challenged to do this. 

As a final experiment, the authors evaluated the LMs on texts where this long-range context is known to be important for word prediction. These texts came from the LAMBADA dataset (Paperno et al., 2016), which also includes “control” texts that do not feature long-range dependencies. Relative to the three Transformer LMs described above, the optimized NPLM fails dramatically on the test set with long-range dependencies but performs only slightly lower on the control set. The failure is not surprising, but the acceptable outcome for the control set shows that NPLMs are not necessarily inadequate for tasks where the input is short. This is insightful because many NLP tasks operate on short sentence-length texts, such as grammatical correction or lexical paraphrasing. These results suggest that self-attention is not the only way to improve models for these tasks. 

In summary

Language models are an increasingly powerful framework for NLP tasks, now driven by neural network architectures with growing size, efficiency, and mathematical complexity. It can be difficult to isolate the impact of various architecture optimizations since they are often introduced concurrently. The self-attention paradigm established a new generation of LMs and consequently a new state-of-the-art for many NLP tasks. The work by Sun & Iyyer (2021) provides evidence that while this paradigm is indeed impactful, LMs also benefit from other advancements outside of self-attention.