Issue #126 - Learning Feature Weights for Denoising Parallel Corpora

Introduction 

Large web-crawled parallel corpora constitute a very useful source of data to improve neural machine translation (NMT) engines. However, their effectiveness is reduced by the large amount of noise they usually contain. As early as in issue #2 of this series, we pointed out that NMT is particularly sensitive to noise in the training data. In issue #21, we presented the dual cross-entropy method to filter out noise in parallel corpora (Junczys-Dowmunt, 2018). In this post, we take a look at a paper by Kumar et al. (2021), which goes a step further and proposes a denoising method combining several sentence-level features with weights learned using reward modeling. 

Method 

The method focuses on learning weights for combining the following sentence-level features: 

• IBM Model 1 (basic word alignment model), 
• source language model, 
• target language model, 
• dual cross-entropy and sentence length ratio. 

The aim of training is to evaluate a reward function R(w|Φ), where w are the weights and Φ is the sentence-level feature vector averaged over a batch of sentences. The optimum weight vector is the one maximizing the reward.

The reward is chosen in a way allowing a direct relation between the value of w and translation performance. This is carried out in an NMT training loop. To sample each batch, the features are calculated for a number of sentence pairs, and the best scoring ones according to a random weight vector are selected. The reward is related to the perplexity of a validation set following a neural network parameter update with the selected batch. The random weight vector, the average feature vector over the batch and the reward calculated in this parameter update constitute one training sample to learn the weight vector. These steps are repeated for a number of batches and the whole procedure is repeated with different candidate NMT runs. 

After having collected enough (weight vector, feature vector, reward) training samples, a simple feed-forward neural network is learned. This neural network maps the input weights (possibly modulated by the batch quality, represented by the feature vector) to the observed reward. The variant with the raw weight vectors as input is referred to as “Weight based”, while the variant in which the weight vectors are scaled by the sum of the corresponding feature vector is referred to as “Feature based”. Once this neural network is learned, a grid search over the weights is performed to find the best weight vector. 

The final step consists of calculating the sentence-level features for each sentence-pair in the corpus, and using the best weight vector to score it. The corpus can then be filtered based on this score.

Experiments

The experiments are performed on the Estonian–English Paracrawl corpus. The Estonian and English language models were trained on their respective NewsCrawl data sets. To compute the dual cross-entropy scores, machine translation models were trained on clean data, namely the Europarl-v8 set. The best weight vector obtained was: dual cross-entropy: 0.81, IBM Model 1: 0.07, Sentence length ratio: 0.07, source language model: 0.03, and target language model: 0.02. These weights were used to score each sentence pair, and three sets, with the best 10, 15 and 20 million (M) English words, were selected. The results are shown in the following table. 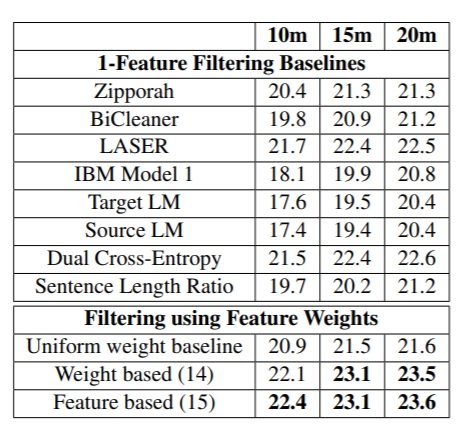The table first shows the BLEU score corresponding to the sets obtained by filtering the corpus with a number of baseline methods. Zipporah, BiCleaner and LASER are three filtering toolkits. The best one in terms of BLEU score is LASER, which is based on pre-trained multilingual embeddings (it could actually be interesting to include LASER as a feature). The rest of the baselines are the individual features. The best scoring one is the dual cross-entropy, which performs similarly as LASER. The very simple sentence length ratio performs surprisingly well, and the monolingual features (language models) perform the worst. The combination of features with uniform weights is worse than the dual cross-entropy. However, with tuned weights, the combination performs between 0.7 to 1 BLEU point better than the best baseline. Scaling the input weights by the sum of the corresponding feature vector (Feature based variant) gives a small improvement. The number in parentheses (14 and 15) are the number of candidate NMT runs for which the best result was achieved. 

Finally, the authors try to transfer the best weight vector to another language pair (Maltese-English paracrawl). However, in that case the combination of features is not better than the dual cross-entropy. This suggests that learning the weight vector is necessary.

In summary

Kumar et al. (2021) propose a parallel corpus filtering (denoising) method which combines the dual cross-entropy feature with four other sentence-level features. The feature weights in the combination are learned based on reward modeling. The training samples are generated in an NMT training loop, with an NMT quality objective related to the perplexity on a validation set. Filtering the corpus based on the feature combination yields slightly better BLEU scores than based on the best baselines, which are the LASER and dual cross-entropy methods. Unfortunately, the best weights learned in one language pair could not be transferred to a different language pair. This method achieves top results, but the calculation of some of the features is slow, as is the process to collect training samples to tune the weights.