Issue #95 - Constrained Parameter Initialisation for Deep Transformers in Neural MT

Introduction 

As the Transformer model is the state of the art in Neural MT, researchers have tried to build wider (with higher dimension vectors) and deeper (with more layers) Transformer networks. Wider networks are more costly in terms of training and generation time, thus they are not the best option in production environments. However, adding encoder layers may improve the translation quality with a very small impact on the generation speed. In this post, we take a look at a paper by Hongfei Xu et al. (2020) which revisits the convergence issues with deep standard Transformer models and proposes a simple solution based on constraining the parameter initialisation. 

Layer normalisation and residual connections 

The advantage of deeper networks is that they can represent more complex functions. However, as already seen in Issue #41 of our blog series, a usual problem for the convergence of deep Transformer network training is vanishing gradients. Vanishing gradients may occur when the network weights are updated. The gradient of the loss function is calculated at each layer. If this involves multiplication of the gradient at previous layers, the result vanishes after a number of layers. 

Two techniques are used to help the training converge: layer normalisation and residual connections. Layer normalisation aims at reducing the variance of sub-layer outputs to have a more stable training. Residual connections are a shortcut from one layer to the next, allowing the information to flow directly, without going through the layer non-linear function.

Order of computation

As highlighted in Issue #41 of our blog series, in the original Transformer paper, layer normalisation LN() was placed after the addition of the residual connection (post-norm, Figure (a))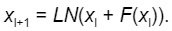 However, in later implementations, layer normalisation was applied to the input of every sub-layer (pre-norm, Figure (b)): 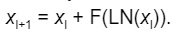The figure is from Wang et al. (2019). 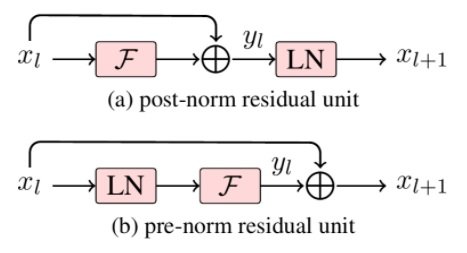Both Wang et al. and Xu et al. report that deep Transformer networks can converge in the pre-norm case, but often not in the post-norm case.

Constrained Parameter Initialisation

Xu et al. go a step further in the analysis of why the training often fails in the post-norm case. They find that it may be because the impact of the residual connection is reduced by the subsequent layer normalisation (we don’t have a direct shortcut from the input to the output of the layer any more). They further find that the residual connection of previous layers is reduced in this case if some parameters are not bounded. Finally, they empirically observe that deep Transformers are only hard to train at the beginning. Thus, only applying a constrained parameter initialisation, in which the required parameters are correctly bounded, is sufficient to achieve convergence in the post-norm case. 

In experiments on the 2014 English-German and 2015 Czech-English tasks of the Workshop on Statistical Machine Translation (WMT), Xu et al. show that the Transformer model training with constrained parameter initialisation converges on the post-norm case (they show results until 24 layers), while 12-layer networks did not converge without it. On the English-German task, the post-norm BLEU score is even slightly better than the pre-norm ones (+0.5 BLEU for 6 and 12 layer networks). 

In Issue #76 of our blog series, we saw that the decoder layers contain somewhat redundant information, thus we can build networks with more encoder layers and less decoder without significantly losing MT quality. Xu et al., on the contrary, observe that thanks to the constrained parameter initialisation, adding more decoder layers helps. They do indeed get similar BLEU scores with 24 encoder and 6 decoder layers as with 6 encoder and 24 decoder layers. These 24-6 or 6-24 encoder-decoder layer configurations are also better than the 6-6 configuration (the Transformer baseline), and worse than the 24-24 configuration.

In summary

This paper gives further insight into the convergence issues of deep transformers. Their proposed method to ensure convergence in the case of the original Transformer definition only implies some constraints on the initial parameters. It can therefore help us to build deeper networks which can represent more complex functions and thus solve more complex problems.